지난 포스팅에서는 단순 이평선 전략의 성과를 확인한 바 있습니다. 이번 포스팅에서는 단순 이평선에서 파생된 지수 이평선 전략과 적응형 이평선 전략의 성과를 확인해보겠습니다.
1. 지수 이평선 전략
단순 이평선이 최근 n일간의 가격 중 특정 가격에 가중치를 두지 않고, 동일하게 평균을 낸 컨셉이라면, 지수 이평선은 최근의 가격 변화에 좀 더 가중치를 두고 계산한 방식입니다.
지수 이평선의 계산식은 아래와 같습니다.
EMA(지수이동평균) = 전일지수이동평균 +{c×(금일종가지수-전일지수이동평균)}
c = 2 / (n+1)
단, 0 < c < 1 ( 9일의 경우 0.2, 12일의 경우 0.15, 26일의 경우엔 가중치 0.075 사용 )
그러면 대체 왜 최근의 가격에 더 가중치를 둘까요?
그 이유는 최근의 가격 변화가 오래 전의 가격보다 더 중요한 정보를 담고 있다는 전제 때문입니다.
예를 들자면, 어떤 학생의 수학 성적의 추세를 볼 때, 최근 3개월 간의 성적과 3년 전의 성적 중 어떤 것이 더 의미가 클까요?
바로 가까운 미래의 움직임은 최근의 데이터와 가격이 더 잘 반영한다고 볼 수 있으므로, 오래 전 데이터보다 최근의 가격에 더 가중치를 두자는 컨셉입니다. 일종의 추세 추종형 철학이 녹아있는 지표라고 할 수 있습니다.
따라서, 똑같이 이동 평균선 돌파 전략을 구사한다고 하면, 단순 이평선 돌파 전략보다 지수 이평선 돌파 전략의 신호가 더 빠르게 잡히는 장점이 있습니다.
'오 그러면, 단순 이평선보다 훨씬 더 좋겠네? '
라고 생각하실 수 있겠지만, 사실은 꼭 그렇지도 않습니다.
그 이유는 신호가 빠르게 잡힌다는게 장점으로 작용할 수도 있겠지만, 단점으로 작용할 수도 있기 때문입니다.
소위 말하는 잘못된 신호 (휩소)가 나타나면 지수 이평선 신호는 괜히 쓸데없이 일찍 들어가고, 쓸데없이 일찍 빠져나오는 소위 전문 용어로 '삑사리'가 나게 되는 것이죠.
이런 경우에는 오히려 단순 이평선보다 못한 결과가 발생하는데요
따라서, 결론은 '딱히 지수 이평선 전략이 단순보다 항상 좋다는 보장 없다'입니다.
지난 포스팅에서 소개한 단순 이평선 포트폴리오를 대상으로 단순 이평선 ---> 지수 이평선으로만 조건을 바꾸어 시뮬레이션 한 결과입니다.
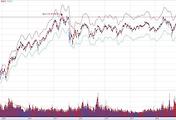
<다중 지수 이평선 돌파 포트폴리오>
단순 이평선 전략과 비교해볼까요?
<다중 단순 이평선 돌파 포트폴리오>
대충 보면 지수 이평선 전략이 약간 더 나은 것 같은데, 큰 차이는 아닙니다.
시장이란게 원래 이렇습니다. 뭔가 업그레이드하고 복잡한 걸 쓰면 더 잘 먹힐 것 같고 엄청나게 업그레이드 될 것 같지만, 꼭 그렇지도 않습니다
2. 적응형 이평선 전략 (Kaufmann's adaptive moving average)
단순 이평선이나 지수 이평선 모두 특정한 n일 값은 고정되어 있습니다.
그런데 적응형 이평선에서는 똑같은 n일 이평선이라도, 시장의 변동성에 따라 고정된 n일 이평선 값에 미세한 조정값이 추가됩니다.
이동 평균선을 추세 추종의 지표로 이용시, 노이즈가 적고 안정된 추세를 보일 경우에는 최근의 가격을 충실히 따라가면 되지만, 오르락 내리락 등락이 심한 경우 최근의 가격은 믿기가 힘들겠지요?
적응형 이평선에는 여러 종류가 있지만 가장 대표적인 것이 유명한 기술적 분석가 Perry Kauffmann이 자신의 유명한 저서인 'Trading systems and method'에서 언급한 Kaufmann's adaptive moving average 입니다.
Kaufmann's adaptive moving average에서는 최근의 가격의 움직임에 노이즈가 적을 때(안정적, 추세적, 작은 변동성)일 경우에는 기본 이평선 시그널에 최근의 가격의 움직임을 적극 반영하고, 노이즈가 클 때 (불안정, 비추세적, 큰 변동성)일 때는 최근의 가격의 움직임을 덜 반영함으로써 좀 더 시장의 움직임을 정확하게 추적하기 위해 노력합니다.
그렇다면 가격의 움직임의 노이즈를 판단하는 기준은 무엇일까요? 이전 포스팅에서도 설명드린 efficiency ratio라는 지표를 이용하여 가격의 노이즈를 정량합니다. Efficiency ratio는 0~1 사이의 값을 가지는데, 1에 가까울수록 안정적, 추세적이고, 0에 가까울수록 불안정하고 비추세적입니다. Efficiency ratio를 이용하여 조정계수라는 값을 산출하여 이동평균선의 값을 보정하는 원리입니다.
이거 참 말로만 설명하려니 어려운데요, 자세한 수식은 여기를 참고하시면 잘 나와 있습니다. 방금 설명드린 개념만 잘 이해하셨다면 수식을 이해하는데도 큰 무리는 없으리라 생각합니다.
ER = Change/Volatility
Change = ABS(Close - Close (10 periods ago))
Volatility = Sum10(ABS(Close - Prior Close))
Volatility is the sum of the absolute value of the last ten price changes (Close - Prior Close).
SC = [ER x (fastest SC - slowest SC) + slowest SC]2
SC = [ER x (2/(2+1) - 2/(30+1)) + 2/(30+1)]2
Current KAMA = Prior KAMA + SC x (Price - Prior KAMA)어떻습니까? 엄청날 것 같죠? 시뮬레이션 결과를 확인해 볼까요?
<다중 KAMA 돌파 포트폴리오>
어떻습니까? 뭐 단순 이평선이랑 비슷한 수준이네요.
이거 왜 이럴까요?
적응형 이평선 전략의 전제 조건은 일반적으로 변동성이 커지면 추세 추종에 불리하다는 전제인데,
이것은 사실이지만, '일반적'이라는 단어가 문제입니다.
'일반적이다'라는 의미는 부정적으로 얘기하면 '안 그럴 때도 꽤 있을 수 있다'는 의미이죠?
'일반적'이라는 것이 통계적으로 딱 떨어진다는 의미도 아니고, 일정한 확률로 항상 그렇다는 것도 아닌 '상당히 두리뭉실'한 개념이기 때문입니다.
시장에서도 이런 속성이 언제 잘 나타날지, 언제 잘 안먹힐지 예측이 불가능합니다.
경우에 따라서는 변동성이 커지는데도, 추세적으로 시장이 움직이는 경우도 허다합니다.
이런 상황에서는 괜히 쓸데없이 고퀄의 지표를 이용해서 삽질한 격이 됩니다.
따라서, 단순 이평선 전략은 '변동성과 추세'에 대해 어떠한 가정도 하지 않았지만, 적응형 이평선 전략은 변동성이 커지면 반드시 시장의 주기가 감소하도록 설정이 되어 있기 때문에 전략 자체는 단순 이평선 전략이 더 간단하고 허접해보이지만, 항상 적응형 이평선 전략이 낫다는 보장은 없습니다.
시장의 움직임이 적응형 이평선 전략의 전제조건에 잘 맞도록 움직여 주는 경우에는 적응형 이평선 전략이 우월한 성과를 보여주겠지만, 그렇지 않고 자기 멋대로 움직이는 경우에는 단순 이평선 전략이 차라리 나은 것이지요.
전략이 복잡할수록 이런 위험성은 더 커지게 되는데요, 단순한 전략이 실제로는 그렇게 단순하지 않다는 철학은 사실 상당히 심오하고, 이를 깊이 깨닫기 위해서는, 깨나 백테스트 좀 돌려봐야 합니다.
그래서 행여나, 제 블로그를 보시는 분들 가운데,
'아니 뭔 전략이 그렇게 단순 무식하게 모멘텀 스코어 딱 하나만 써? 없어 보이게? 미분 방정식 같은 것도 집어 넣고, 각종 신호처리, 시계열 분석 기반 최첨단 필터도 집어 넣어야 알파고 시대에 살아남는거 아냐?'
라고 생각하실 지 모르겠으나, 복잡한 전략이 꼭 좋다는 보장은 없다는 점, 그리고 여기에는 분명한 이유가 있다는 점을 아셨으면 좋겠습니다.
3. 딱히 영양가도 없는 걸 왜 소개하냐?
'아니 대체 그런 맥빠진 결론을 낼 거면 대체 왜 이런 걸 소개하냐? 시장에서 좀 잘 먹히는 걸 알려달라고! 이건 시간 낭비잖아?'
라고 생각하실런지 모르지만,
굳이 별 의미없어 보이는 내용까지 알려드리는 이유는
여러분이 시장에서 어떤 전략이 잘 먹히는지 알기 위해서는 반드시, 어떤 전략이 잘 안먹히는지도 잘 알아야 하기 때문입니다.
그래야만 '절대적인 수익 전략'으로 현혹시키는 사기꾼들의 농간에 당하지 않을 수 있습니다.
이런 검증 과정을 통해서, 왜 우리의 상식과 직관과 다르게 성과가 생각보다 잘 나오지 않는지를 분석할 수 있고 이는 좀 더 좋은 전략을 개발하는 중요한 밑거름이 됩니다.
그래서, 역설적으로 좋은 전략을 개발하기 위해서는 반드시 이런 무수한 실패의 결과물도 많이 만들어 보아야 하고, 이를 통해 오히려 더 많은 것들을 배울 수가 있습니다.
앞으로 소개해드릴 전략 중에도 별 영양가 없어 보이는 것들이 상당히 많이 있는데요,
의미 없다고 무시하지 마시고, 의미 없어보이는 결과에서 '의미 있는 것'을 많이 발견하시기 바랍니다.
< 나가시기 전에 블로그 글 맨 하단의 배너 광고를 한 번만 클릭해주시면 더 좋은 콘텐츠를 만드는데 큰 도움이 됩니다~ 감사합니다! >
1. 네이버 카페 '실전주식투자 연구소' (클릭) 으로 오시면, 본 블로그의 모든 내용을 순서대로 확인하실 수 있고, 다양한 실전 투자 정보도 얻을 수 있습니다~
2. 'systrader79의 주식 단기 매매 전략 온라인 강좌'가 뉴지스탁에서 진행 중입니다!
개별 주식을 이용한 단기 매매 기법, 뉴지스탁을 통한 완전 자동 투자 매매 구현에 관한 폭넓 은 노하우를 다루고 있으니, 많은 성원 부탁드립니다~
첫 번째 강의는 수강 신청없이 무료로 시청 가능합니다 (아래 링크 클릭 --> 1번 방송 클릭)
3. 여러분의 인생이 걸린 너무나도 중요한 소식! --- > 여기를 클릭하세요!
'systrader79 칼럼 > 실전 투자 전략' 카테고리의 다른 글
| 실전 투자 전략 (39) - 역추세 전략, RSI(2) system (3) | 2017.04.04 |
|---|---|
| 실전 투자 전략 (38) - 채널 돌파 전략 (0) | 2017.04.01 |
| 실전 투자 전략 (37) - 채널 돌파 전략의 개요 (2) | 2017.03.30 |
| 실전 투자 전략 (36) - 모멘텀 전략 (0) | 2017.03.29 |
| 실전 투자 전략 (35) - 단순 이평선 돌파 전략 (1) | 2017.03.26 |
| 실전 투자 전략 (34) - Techinical trading 기법 시리즈를 시작하며 (1) | 2017.03.17 |
| 실전 투자 전략 (33) - MPAA 전략 stress test (4) | 2017.02.28 |
| 실전 투자 전략 (32) - 동적 자산 배분 전략의 몰락? (4) | 2017.02.27 |









댓글