실전 투자 전략 (31) - Modified PAA model을 이용한 절대 수익 전략 (4)

 이번 포스팅에서는 지난 번에 살펴보았던 MPAA 절대 수익 전략을 조금 변형, 가공한 방법을 알아보겠습니다. 

 MPAA 전략에 대한 상세한 내용은 다음 링크를 순서대로 참고해주시기 바랍니다. 

 MPAA 전략 (1)

 MPAA 전략 (2)

 MPAA 전략 (3)

시작하기에 앞서, 기존에 제시했던 MPAA 전략의 로직을 간단하게 리뷰하고, 변형된 MPAA 전략에 대해 살펴보겠습니다. 

1. 기존의 MPAA 전략 순서 

  * 순서 : 절대 모멘텀 -->  수익 곡선 모멘텀 ---> 상대 모멘텀 ---> 자산군 비중 배분

  1 단계 : 투자 유니버스 및 투자 종목 선정

    ex ) 주식 : S&P500, KOSPI200, Nikkei225, Eurostoxx50 등

         채권 : 10년 만기 국고채, 하이일드 채권 등

         현금 : 3년 만기 국고채

         기타 : 금, 원유, 상품 index 등

  2 단계 : 각 종목에 평균 모멘텀 스코어 + 현금 혼합 전략 적용 (절대 모멘텀 컨셉 전략)

  3 단계 : 2 단계의 수익 곡선에 수익곡선 모멘텀 전략 적용 (6개월 수익곡선 모멘텀)

  4 단계 : 3 단계의 수익 곡선에 상대 모멘텀 적용 (1~12개월 평균 모멘텀 상위 n개 종목 선정)

  5 단계 : 4 단계 수익 곡선들에 대해 자산군 비중 배분 비율 적용

  즉, 기존 전략은 수익 곡선 모멘텀까지 다 적용한 절대 수익 curve를 대상으로 상대 모멘텀을 적용하는 방식이었습니다. 

 이 방법의 장점은 수익 곡선 모멘텀이 무조건 먼저 적용된 상태이기 때문에 현금 배분 비중이 구조적으로 높아, drawdown이 매우 낮아 아주 안정적인 장기 수익 곡선을 기대할 수 있다는 점입니다. 

 그런데, 이 방법은 오리지널 듀얼 모멘텀 전략과는 순서가 약간 다릅니다. 오리지널 듀얼 모멘텀 전략은 모멘텀이 가장 큰 종목을 먼저 정하고, 그 후 절대 모멘텀 < 0 인 종목은 현금으로 대치하는 순서이지요? 

 모멘텀 전략이라는 것은 결국은 추세 추종이기 때문에 수익곡선 모멘텀까지 다 적용한 상태에서 상대 모멘텀을 적용해도 상관은 없지만, 본래 듀얼 모멘텀 전략의 취지에 좀 더 충실하기 위해서는 일단 듀얼 모멘텀 전략을 먼저 구사한 후 최종적으로 나타난 수익 곡선에 수익 곡선 모멘텀을 적용해야 하겠지요? 

 이런 논리에 입각하여 MPAA 전략을 좀 더 본질적인 듀얼 모멘텀 컨셉에 가깝게 변형시키면 다음과 같습니다. 순서만 약간 바뀝니다. 

2. 변형된 MPAA 전략 (오리지널 듀얼 모멘텀 전략에 보다 충실)

 * 순서 : 상대 모멘텀 --> 절대 모멘텀 --> 자산군 비중 배분 --> 수익 곡선 모멘텀

  1 단계 : 투자 유니버스 및 투자 종목 선정

    ex ) 주식 : S&P500, KOSPI200, Nikkei225, Eurostoxx50 등

         채권 : 10년 만기 국고채, 하이일드 채권 등

         현금 : 3년 만기 국고채

         기타 : 금, 원유, 상품 index 등

  2 단계 : 1~12개월 평균 모멘텀 기준으로 상대 모멘텀 상위 종목 선정 (상대 모멘텀) 

  3 단계 : 선정된 종목 대상으로 평균 모멘텀 스코어 + 현금 혼합 전략 적용 (절대 모멘텀)

  4 단계 : 3 단계의 수익 곡선에 자산군 비중 배분 비율 적용

  5 단계 : 4 단계 수익 곡선에 최종적으로 수익 곡선 모멘텀 적용 (6개월 수익곡선 모멘텀)

 변형된 MPAA 전략의 장점은 두 가지입니다. 

 첫째, 앞서 설명드린 바와 같이 본질적인 듀얼 모멘텀 전략의 컨셉에 좀 더 충실하다.

 둘째, 수익 곡선 모멘텀이 가장 나중에 한 번만 적용되기 때문에, 현금 비중이 근소하게 줄어 평균 수익률이 기존 방식보다 살짝 더 올라간다.

 사실, 평균 모멘텀 스코어 + 현금 혼합만 해도 drawdown이 상당히 줄어들고 충분히 안정적인 구조이기 때문에, 안정성을 더 높이기 위해 굳이 모든 자산에 강제적으로 수익 곡선 모멘텀을 다 적용할 필요는 없습니다. 

 그렇기 때문에, 이 방법을 이용하면 이론적으로나 시뮬레이션상에서나 CAGR이 조금 더 올라가는 것을 확인할 수 있습니다. 

3. 그렇다면 결론은? 

 첫 번째 방법이나 두 번째 방법 모두 퍼포먼스는 거의 유사합니다. 

 굳이 차이점을 말씀드리면 첫 번째 방법은 근소하나마 안정성이 상대적인 장점이고, 두번째 방법은 수익성이 상대적으로 낫다는 점입니다. 

 백테스트를 동일한 조건에서 해보면, 조건에 따라 다르지만 상대적인 CAGR이나 MDD는 장기적으로 0.5~1% 상대적으로 차이가 나는 수준입니다. 경우에 따라서는 두 번째 방법이 MDD나 CAGR 모두 우수한 경우도 있습니다.  

 (ex : MPAA1 : CAGR 8% / MDD : -5% , MPAA 2 : CAGR 9% / MDD -6% )

 개인적으로는 성공 투자의 핵심은 투자 수익의 변동성과 리스크를 최대한 줄이는 거라고 보는 입장인데, 수십년간의 투자 시계열에서 MDD가 -5% 수준으로 지극히 낮은 수준에서 1% 정도 차이가 나는 관점이라면 두 번째 MPAA 전략이 장기적으로는 안정성을 거의 훼손하지 않으면서 조금이나마 수익률을 더 높이는 방법이라고 생각합니다. 

4. 변형된 MPAA 전략 코드 

 코드는 다음과 같습니다. 코드 시뮬레이션 방법은 이전 포스팅(클릭)을 참고해주시기 바랍니다. 

 이번 시뮬레이션에서는 주식을 국가, 섹터, 팩터로 나누지 않고 전체를 하나로 합쳐 한 개의 자산군으로 테스트했고, 수익곡선 모멘텀 기간도 12개월이 아닌 6개월로 단축시켜 시뮬레이션 해 보았습니다. 

 파이썬 노트북 파일과 엑셀 파일은 카페 자료실(클릭)에서 다운받으실 수 있습니다. 

#1. 데이터 가져오기

import pandas as pd

import matplotlib.pyplot as plt

import numpy as np

import pandas_datareader.data as web

import matplotlib

matplotlib.rc('font', family='Malgun Gothic',size=8, weight = 'bold')

파일 = pd.ExcelFile('N:\투자시뮬\포트폴리오 데이터 가공 (통합).xlsx')

자산군 = 파일.sheet_names

자산군

#2. 자산군별 데이터 프레임 설정

자료 = {}

for i in 자산군:

    자료[i] = 파일.parse(i)

    자료[i].index = 자료[i].날짜

    자료[i].drop('날짜', axis = 1, inplace=True)

    print(i+'개수',len(자료[i].columns))

#3. 함수 설정

def 월간수익률(데이터):

    return 데이터 / 데이터.shift(1)

def 변동성대비모멘텀(데이터):

    a = 데이터/데이터.shift(12)

    b = 월간수익률(데이터).rolling(12).std()

    return a/b

def 연평균수익률(데이터):

    return 데이터/데이터.shift(12)

def 평균모멘텀(데이터):

    초기값 = 0

    for i in range(1, 13):

        초기값 = 데이터 / 데이터.shift(i) + 초기값

    return 초기값 / 12

def 모멘텀순위(데이터, 순위):

    x = 평균모멘텀(데이터)

    y = x.iloc[ : , 0: len(x.columns)].rank(1, ascending=0)

    y[y <= 순위] = 1

    y[y > 순위] = 0

    return y

def 평균모멘텀스코어(데이터):

    a = 평균모멘텀(데이터).copy()

    초기값 = 0

    for i in range(1, 13):

        초기값 = np.where(데이터 / 데이터.shift(i) > 1, 1, 0) + 초기값

    a[a > -1] = 초기값/12

    return a

def 평균모멘텀스코어6(데이터):

    a = 평균모멘텀(데이터).copy()

    초기값 = 0

    for i in range(1, 7):

        초기값 = np.where(데이터 / 데이터.shift(i) > 1, 1, 0) + 초기값

    a[a > -1] = 초기값/6

    return a

def 현금혼합모멘텀수익곡선(데이터, 현금비율=1):

    x = 월간수익률(자료['현금'])*현금비율

    a = pd.DataFrame((월간수익률(데이터).values*평균모멘텀스코어(데이터).shift(1).values+x.values)/(현금비율+평균모멘텀스코어(데이터).shift(1).values)).cumprod() 

    a.index = 데이터.index

    a.columns = 데이터.columns

    return a

def 자산군통합포트(데이터, 순위, 자산군비중):

    x = 월간수익률(현금혼합모멘텀수익곡선(데이터))

    y = np.where(모멘텀순위(데이터, 순위).shift(1)==0,np.nan,자산군비중/순위)

    z = ((x*y).sum(1)).dropna()

    z = z.replace(0, np.nan)

    return z

def 통합모멘텀(국가비중,섹터비중,팩터비중,채권비중):

    a = 자산군통합포트(자료['국가'],6,국가비중)

    b = 자산군통합포트(자료['섹터'],4,섹터비중)

    c = 자산군통합포트(자료['팩터'],2,팩터비중)

    d = 자산군통합포트(자료['채권'],1,채권비중)

    e = (pd.concat([a, b, c, d], axis=1).sum(1)/(국가비중+섹터비중+팩터비중+채권비중))

    e = e.replace(0,np.nan).cumprod()

    e.columns = ['통합수익']

    return e

def 수익곡선모멘텀(국가비중,섹터비중,팩터비중,채권비중):

    x = 월간수익률(자료['현금'])

    y = pd.DataFrame(통합모멘텀(국가비중,섹터비중,팩터비중,채권비중), index = x.index)    

    a = pd.DataFrame((월간수익률(y).values*평균모멘텀스코어6(y).shift(1).values+(1-평균모멘텀스코어6(y).shift(1).values)*x.values), index = x.index).cumprod().dropna()

    return a

#4. 결과 plot

# 국가, 섹터, 팩터, 채권

a = 수익곡선모멘텀(1,0,0,1)

b = 자료['국가'].한국/자료['국가'].한국.ix[0]

c = pd.concat([a, b], axis=1).dropna()

c.columns = ['포트폴리오', '코스피']

c.divide(c.ix[0]).plot(figsize = (8,6))

plt.show()

#5. MDD

최대하락 = c.포트폴리오.rolling(min_periods=1, window = 500).max()

당월하락 = c.포트폴리오/최대하락 - 1.0

최대하락폭 = 당월하락.rolling(min_periods=1, window=500).min()

당월하락.plot(subplots=True, figsize = (8,2), linestyle='dotted')

최대하락폭.plot(subplots=True, figsize = (8,2), color = 'red', linestyle='dotted')

plt.show()

#6. MDD / CAGR

투자기간 = len(c.index)/12

print("MDD : "+str(최대하락폭.min()*100)[0:5]+"%")

print("CAGR : "+str(c.포트폴리오[-1]**(1/투자기간)*100-100)[0:4]+"%")

5. 결과

 투자 그룹 : 위험자산군 - 19 종목 (주식, 팩터, 섹터 모두 하나로 통합)

               안전 자산군 - 10년 만기 국고채

               현금 - 3년 만기 국고채

 위험자산군 중 모멘텀 상위 6개 선정, MPAA 전략 1 (기존 방식), MPAA 전략 2 (새로운 방식) 적용

 위험자산과 안전자산의 asset class 비중은 1:1 (보수적인 투자 모델)로 시뮬레이션

 

  <MPAA 1>

 <MPAA 2>

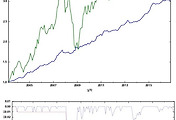
 전체적인 투자 성과는 두 방법 간에 큰 차이는 없으나, 지금 테스트한 시뮬레이션 조건 하에서는 MPAA 2 전략이 리스크와 연평균 수익률 모두 근소하게 우세한 것으로 확인되었습니다. 

 장기수익곡선상, MPAA1 로직은 장기적으로 코스피를 상회하나 MPAA2 성과는 떨어지는 것처럼 보이나, 이는 로직 계산 순서상 시뮬레이션 시작 시점에 차이가 발생하여 나타난 결과입니다. 

 현금 비중을 없애고, 채권에도 분산투자하지 않는 주식 몰빵형으로 돌려보면 어떤 결과가 나올까요? 아래와 같이 일반적인 듀얼 모멘텀 전략과 비슷한 수익 곡선이 나옵니다.

 

 연평균 수익률이 거의 20%에 육박합니다. 하지만, MDD도 -20%를 넘어가고 빨간 박스에서와 같은 장기 손실구간을 고려한다면, 이런 투자를 장기간 할 사람은 별로 없겠지요? 

 그래도 구조적으로 최소한의 추세 기반 리스크 관리 로직은 포함되어 있기 때문에 최악의 하락장은 피하는 구조라 장기적으로는 주식 100%에 바이앤홀딩하는 투자법과 비교하면, 이보다는 훨씬 더 높은 수익률과 안정성을 기대할 수 있습니다. 

 

 이처럼 MPAA 전략은 현금 혼합 비중, 안전 자산과의 배분비, 상대 모멘텀 상위 종목 선정 개수 같은 옵션을 마음대로 조절할 수 있고 그에 따라 개인의 투자 성향에 맞게 얼마든지 장기 투자 수익률과 리스크를 조절할 수 있는 장점이 있습니다. 

 다음 번 포스팅에서는, MPAA 전략의 성과가 안정적으로 나오는 이유가 지표값의 최적화에 의한 것인지, 구조적인 안정성에 의한 것인지 확인하기 위해 디폴트로 지정된 값들을 다른 값들로 바꾸었을 때 전체 시스템 성과에 어떤 변화가 발생하는지 확인해보겠습니다. 

 지표값들을 길거나 짧게 변화시켰을 때, 성과가 크게 바뀐다면, 이는 로직에 심각한 과최적화의 문제가 있다는 것을 의미하고, 지표값을 아무리 변화시켜도 시스템의 성과에 큰 변화가 없다면 이는 향후 시장이 어떤 방식으로 변한다고 하더라도 장기적으로 믿을만한 시스템임을 확인할 수 있기 때문이지요.

 이와 더불어, 동적 자산 배분 전략의 효시라고 할 수 있는 IVY 포트폴리오 로직의 최근 성과의 비교를 통해, 동적 자산 배분 전략의 단점은 없는지, 이를 극복하기 위한 방법은 무엇인지도 살펴보겠습니다. 

< 나가시기 전에 블로그 글 맨 하단의 배너 광고를 한 번만 클릭해주시면 더 좋은 콘텐츠를 만드는데 큰 도움이 됩니다~ 감사합니다! >

1. 블로그에서 다룰 급등주 자동 매매 프로그램을 공개적으로 만들고 있습니다. 관심 있으신 분은 여기를 클릭하셔서 회원가입해 주세요~

2. 본 블로그에 소개된 시황과 무관한 절대 수익 전략을 이용한 ETF 투자 상품을 출시하려고 합니다. 자세한 정보는 여기를 클릭하시기 바랍니다

3. 여러분의 인생이 걸린 너무나도 중요한 소식! --- > 여기를 클릭하세요!